그래프에서 최소 비용 문제?
1) 모든 정점을 연결하는 간선들의 가중치의 합이 최소가 되는 트리
2) 두 정점 사이의 최소 비용의 경로 찾기
신장 트리
: n개의 정점으로 무방향 그래프에서 n개의 정점과 n-1개의 간선으로 이루어진 트리
-> 사이클 x, 하지만 모든 정점이 연결된
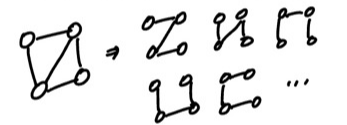
최소 신장 트리
: 무방향 가중치 그래프에서 신장 트리를 구성하는 간선들의 가중치의 합이 최소인 신장 트리
MST를 표현하는 방법
'''
6 11
0 1 32
0 2 31
0 5 60
0 6 51
1 2 21
2 4 46
2 6 25
3 4 34
3 5 18
4 5 40
4 6 51
'''
# V : 노드의 개수, E : 간선의 개수
V, E = map(int, input().split())
# 인접 행렬
adjM = [[0] * (V+1) for _ in range(V+1)]
# 인접 리스트
adjL = [[] for _ in range(V+1)]
for _ in range(E):
u, v, w = map(int, input().split())
adjM[u][v] = w
adjM[v][u] = w # 가중치가 있는 무방향 그래프
adjL[u].append((v, w))
adjL[v].append((u, w)) # 가중치가 있는 무방향 그래프
'''
인접 랭렬
[ [0, 32, 31, 0, 0, 60, 51],
[32, 0, 21, 0, 0, 0, 0],
[31, 21, 0, 0, 46, 0, 25],
[0, 0, 0, 0, 34, 18, 0],
[0, 0, 46, 34, 0, 40, 51],
[60, 0, 0, 18, 40, 0, 0],
[51, 0, 25, 0, 51, 0, 0] ]
인접 리스트
[[(1, 32), (2, 31), (5, 60), (6, 51)],
[(0, 32), (2, 21)],
[(0, 31), (1, 21), (4, 46), (6, 25)],
[(4, 34), (5, 18)],
[(2, 46), (3, 34), (5, 40), (6, 51)],
[(0, 60), (3, 18), (4, 40)],
[(0, 51), (2, 25), (4, 51)]]
'''
Prim 알고리즘
: 하나의 정점에서 연결된 간선들 중에 하나씩 선택하면서 MST를 만들어 가는 방식
1) 임의 정점을 하나 선택해서 시작
2) 선택한 정점과 인접하는 정점들 중의 최소 비용의 간선이 존재하는 정점을 선택
3) 모든 정점이 선택될 때까지 1, 2의 과정을 반복
구현
'''
6 11
0 1 32
0 2 31
0 5 60
0 6 51
1 2 21
2 4 46
2 6 25
3 4 34
3 5 18
4 5 40
4 6 51
'''
def prim():
U = []
# 최소 비용을 담을 배열
D = [10000] * (N + 1)
P = [10000] * (N + 1)
# 첫번째 원소를 선택할 수 있도록
D[0] = 0
# 모든 정점을 다 방문할 때까지 반복
while len(U) < (N+1):
# D중 가장 작은 값을 가진 정점을 선택
minV = 10000
for i in range(N+1):
# 이미 트리에 포함되어 있으면 수행할 필요 없어
if i in U : continue
if minV > D[i]:
minV = D[i]
curV = i
U.append(curV)
# curV하고 연결된 정점들의 D값을 최선으로 변경
for i in range(N+1):
# 이미 트리에 포함되어 있으면 수행할 필요 없어
if i in U : continue
# 연결되어 있고(G[curV][i] > 0), 비용이 최소이면
if G[curV][i] and D[i] > G[curV][i]:
# 최소 비용을 갱신하기
D[i] = G[curV][i]
P[i] = curV
print(f'방문순서(U) : {U}')
print(f'선택된 간선의 가중치(D) : {D}')
print(f'연결된 노드의 인덱스(P) : {P}')
N, E = map(int, input().split())
# 인접 행렬
G = [[0] * (N+1) for _ in range(N+1)]
for _ in range(E):
u, v, w = map(int, input().split())
G[u][v] = w
G[v][u] = w # 가중치가 있는 무방향 그래프
prim()
'''
방문순서(U) : [0, 2, 1, 6, 4, 3, 5]
선택된 간선의 가중치(D) : [0, 21, 31, 34, 46, 18, 25]
연결된 노드의 인덱스(P) : [10000, 2, 0, 4, 2, 3, 2]
'''



요 몇 일 동안은 하늘 사진을 못찍었넹..ㅎ
홀로 샌프란 여행 중 가장 기억에 남았던, 자전거 타고 금문교!
소샬리토에서 먹은 민초 아이스크림도 생각나.. 꼭 다시 가보고싶다
'Algorithm' 카테고리의 다른 글
| 서로소 집합(Disjoint-sets) (0) | 2022.09.29 |
|---|---|
| 최단 경로 - Dijkstra (0) | 2022.09.28 |
| 이진 검색 (0) | 2022.09.27 |
| 퀵 정렬 (0) | 2022.09.26 |
| 병합 정렬 (0) | 2022.09.26 |




댓글