트리
: 비선형 구조. 그래프의 특수한 경우. 원소들 간에 계층관계를 가지는 계층형 자료구조.
-> 상위 원소에서 하위원소로 내려가며 확장되는 모습
트리를 사용하는 가장 큰 이유는 문제를 해결할 때 subtree 로 나누어서 접근 할 수 있기 때문 (재귀적 정의)
degree
1. 노드의 차수 : 노드에 연결된 자식 노드의 수2. 트리의 차수 : 노드의 차수 중 가장 큰 수-> 실제로 구현했을 때 공간(차원)을 미리 잡을 수 있는 정보가 된다
이진트리
: 모든 노드들이 2개의 서브트리를 갖는 특별한 형태의 트리
- 각 노드가 자식 노드를 최대 2개 까지만 가질 수 있는 트리
특징)
1. 레벨 i 에서 노드의 최대 개수는 2^i
2. 높이가 h인 이진 트리가 가질 수 있는 노드의 최소 개수는 (h+1)개가 되며, 최대는 (2^(h+1) -1)개
종류)
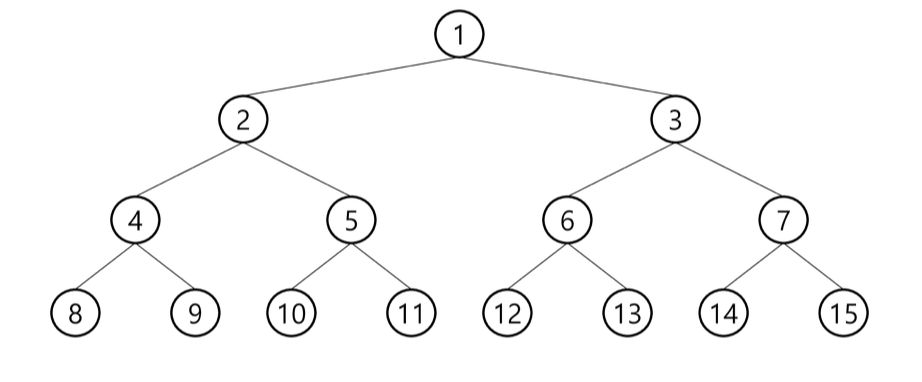
1. 포화 이진 트리
: 모든 레벨에 노드가 포화상태로 차 있는 이진 트리
- 높이가 h일 때, 최대 노드 개수인 (2^(h+1) -1)의 노드를 가진 이진 트리
- 루트를 1번으로 하여 (2^(h+1) -1)까지 정해진 위치에 대한 노드 번호를 가짐
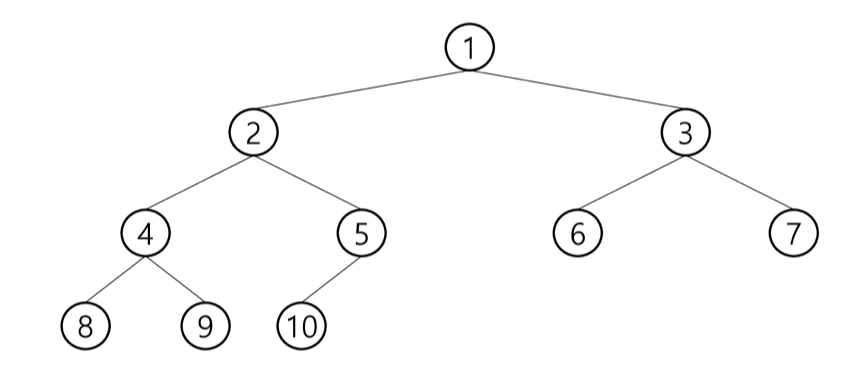
2. 완전 이진 트리
: 높이가 h이고 노드 수가 n개일 때 (단, h+1 <= n < 2^(h+1) -1), 포화 이진 트리의 노드 번호 1번부터 n번까지 빈 자리가 없는 이진 트리
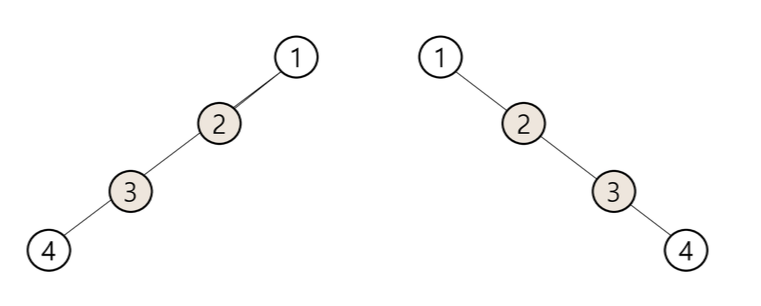
3. 편향 이진 트리
: 높이 h에 대한 최소 개수의 노드를 가지면서 한쪽 방향의 자식 노드만을 가진 이진 트리
- 오른쪽 편향 이진 트리, 왼쪽 편향 이진 트리
Traversal(순회)
: 트리의 각 노드를 중복되지 않게 전부 방문하는 것을 말하는데 트리는 비 선형 구조이기 때문에 선형구조에서와 같이 선후 연결 관계를 알 수 없다.
- 따라서 특별한 방법 필요하다.
1. Preorder traversal (전위순회)
알고리즘)

# 전위순회
def preorder_traverse(T):
if T: # T is not None
visit(T)
preorder_traverse(T.left)
preorder_traverse(T.right)2. Inorder traversal (중위순회)
알고리즘)
# 중위순회
def inorder_traverse(T):
if T: # T is not None
inorder_traverse(T.left)
visit(T)
inorder_traverse(T.right)3. Postorder traversal (후위순회)
알고리즘)
# 후위순회
def postorder_traverse(T):
if T: # T is not None
postorder_traverse(T.left)
postorder_traverse(T.right)
visit(T)
배열을 이용한 이진 트리의 표현
배열을 이용한 이진 트리 표현의 단점)
: 편향 이진 트리의 경우에 사용하지 않는 배열 원소에 대한 메모리 공간 낭비 발생
- 트리의 중간에 새로운 노드를 삽입하거나 기존의 노드를 삭제할 경우 배열의 크기 변경이 어려워 비효율적임
-> 연습문제에서는 이차원 배열을 이용하여 부모노드(인덱스 번호)와 자식노드를 표현한다.
ex) [ [왼쪽 자식노드, 오른쪽 자식노드] ] >>> 이때 안쪽 리스트의 인덱스가 부모 노드의 번호가 된다.
연습문제
Q. 다음 이진트리 표현에 대하여 순회하여 정점의 번호를 출력하시오.
1 2 1 3 2 4 3 5 3 6 4 7 5 8 5 9 6 10 6 11 7 12 11 13# 전위순회
def preorder_traverse(root):
if root != 0:
print(root, end=' ')
preorder_traverse(tree[root][0])
preorder_traverse(tree[root][1])
# 중위순회
def inorder_traverse(root):
if root != 0:
inorder_traverse(tree[root][0])
print(root, end=' ')
inorder_traverse(tree[root][1])
# 후위순회
def postorder_traverse(root):
if root != 0:
postorder_traverse(tree[root][0])
postorder_traverse(tree[root][1])
print(root, end=' ')
# 연습문제
inputS = '1 2 1 3 2 4 3 5 3 6 4 7 5 8 5 9 6 10 6 11 7 12 11 13'
lst = list(map(int, inputS.split()))
# print(lst)
V = 13
# 빈 트리 만들기
tree = [[0, 0] for _ in range(V+1)]
# 역으로 조회하기 위한 부모노드의 정보
parent = [0]* (V+1)
for i in range(0, len(lst),2):
p, c = lst[i], lst[i+1]
# 왼쪽 자식노드가 비어있으면 왼쪽에
if tree[p][0] == 0:
tree[p][0] = c
# 아니면 오른쪽에
else:
tree[p][1] = c
# 자식노드의 부모노드 번호 저장
parent[c] = p
preorder_traverse(1)
print()
inorder_traverse(1)
print()
postorder_traverse(1)
print()
'''
1 2 4 7 12 3 5 8 9 6 10 11 13
12 7 4 2 1 8 5 9 3 10 6 13 11
12 7 4 2 8 9 5 10 13 11 6 3 1
'''
SWEA_1231. 중위순회
다음은 특정 단어(또는 문장)를 트리 형태로 구성한 것으로, in-order 형식으로 순회하여 각 노드를 읽으면 원래 단어를 알 수 있다고 한다.
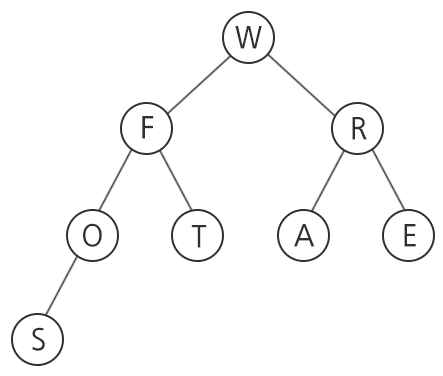
위 트리를 in-order 형식으로 순회할 경우 SOFTWARE 라는 단어를 읽을 수 있다.
[제약 사항]
총 10개의 테스트 케이스가 주어진다.
총 노드의 개수는 100개를 넘어가지 않는다.
트리는 완전 이진 트리 형식으로 주어지며, 노드당 하나의 알파벳만 저장할 수 있다.
노드가 주어지는 순서는 아래 그림과 같은 숫자 번호대로 주어진다.
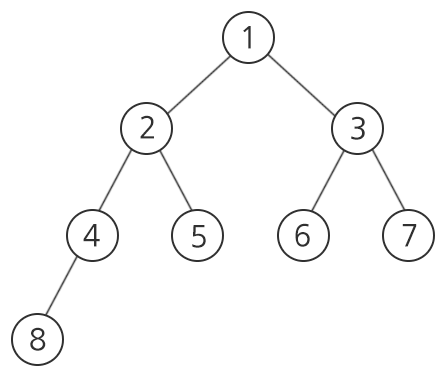
[입력]
각 테스트 케이스의 첫 줄에는 각 케이스의 트리가 갖는 정점의 총 수 N(1≤N≤100)이 주어진다. 그 다음 N줄에 걸쳐 각각의 정점 정보가 주어진다.
해당 정점에 대한 정보는 해당 정점의 알파벳, 해당 정점의 왼쪽 자식, 오른쪽 자식의 정점번호가 차례대로 주어진다.
정점번호는 1부터 N까지의 정수로 구분된다. 입력에서 정점 번호를 매기는 규칙은 위와 같으며, 루트 정점의 번호는 반드시 1이다.
입력에서 이웃한 알파벳이나 자식 정점의 번호는 모두 공백으로 구분된다.
위의 예시에서, 알파벳 S가 7번 정점에 해당하면 “7 S”으로 주어지고, 알파벳 ‘F’가 2번 정점에 해당하면 두 자식이 각각 알파벳 ‘O’인 4번 정점과 알파벳 ‘T’인 5번 정점이므로 “2 F 4 5”로 주어진다.
총 10개의 테스트 케이스가 주어진다,
[출력]
#부호와 함께 테스트 케이스의 번호를 출력하고, 공백 문자 후 테스트 케이스의 답을 출력한다.
import sys
sys.stdin = open('1231_input.txt', 'r')
def inorder(root):
if root:
if len(tree[root]) == 1:
print(tree[root][0], end='')
if len(tree[root]) == 2:
inorder(int(tree[root][1]))
print(tree[root][0], end='')
if len(tree[root]) == 3:
inorder(int(tree[root][1]))
print(tree[root][0], end='')
inorder(int(tree[root][2]))
for test_case in range(1, 11):
N = int(input())
tree = [['', 0, 0]]
for n in range(N):
tmp = input().split()
tree.append(tmp[1:])
# print(tree)
print(f'#{test_case}', end=' ')
inorder(1)
print()
아직 아가 수준의 트리 문제 인것 같긴 하지만 나름 재밌군,,,ㅎㅎ
나중에도 재밌었으면,,,,좋겠...을리가 없다
재귀 시러

좋은 사람 앞에서 한없이 좋은 사람이고 싶은 마음이 있다.
동시에 그렇지 않은 사람에게도 관대한 사람이고 싶다. 그게 제일 어려움.
+ 나는 해야할 말을 하는 것보다 하지 말아야 하는 말을 하지 않는 사람이 되어야지.




댓글