SWEA_1248_공통조상
SW Expert Academy
SW 프로그래밍 역량 강화에 도움이 되는 다양한 학습 컨텐츠를 확인하세요!
swexpertacademy.com
문제
이진 트리에서 임의의 두 정점의 가장 가까운 공통 조상을 찾고, 그 정점을 루트로 하는 서브 트리의 크기를 알아내는 프로그램을 작성하라.
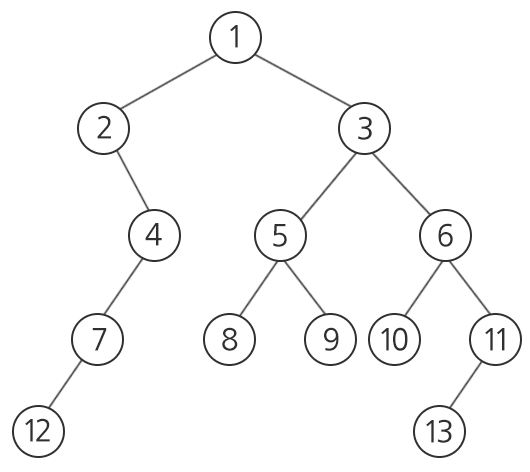
예를 들어, 위의 이진 트리에서 정점 8과 13의 공통 조상은 정점 3과 1 두 개가 있다.
이 중 8, 13에 가장 가까운 것은 정점 3이고, 정점 3을 루트로 하는 서브 트리의 크기(서브 트리에 포함된 정점의 수)는 8이다.
입력
가장 첫 번째 줄에 테스트케이스의 수가 주어진다.
각 케이스의 첫 번째 줄에는 정점의 개수 V(10 ≤ V ≤ 10000)와 간선의 개수 E, 공통 조상을 찾는 두 개의 정점 번호가 주어진다.
각 케이스의 두 번째 줄에는 E개 간선이 나열된다. 간선은 항상 “부모 자식” 순서로 표기된다.
위에서 예로 든 트리에서 정점 5와 8을 잇는 간선은 “5 8”로 표기된다.
정점의 번호는 1부터 V까지의 정수이며, 루트 정점은 항상 1번이다.
출력
각 테스트케이스마다 '#t'(t는 테스트케이스 번호를 의미하며 1부터 시작한다)를 출력하고, 가장 가까운 공통 조상의 번호와 그것을 루트로 하는 서브 트리의 크기를 공백으로 구분하여 출력하라.
코드
import sys
sys.stdin = open('1248_input.txt', 'r')
def subtreeCnt(n):
global cnt
# 노드가 존재하지 않으면 아무것도 리턴하지 않음
if n == 0:
return
cnt += 1
subtreeCnt(c1[n])
subtreeCnt(c2[n])
T = int(input())
for test_case in range(1, T+1):
V, E, n1, n2 = map(int, input().split())
# '부모 자식' 순서로 표현된 간선
lst = list(map(int, input().split()))
# 자식노드 저장
c1 = [0] * (V + 1)
c2 = [0] * (V + 1)
# 부모노드 저장
par = [0] * (V+1)
for i in range(0, len(lst), 2):
if c1[lst[i]] == 0:
c1[lst[i]] = lst[i+1]
else:
c2[lst[i]] = lst[i + 1]
# 자식노드의 부모노드 인덱스 저장
par[lst[i+1]] = lst[i]
# n1의 부모노드 추척
p1 = []
while 1 < n1:
p1.append(par[n1])
n1 = par[n1]
# n2의 부모노드 추적,,하면서 가장 가까운 공통조상 찾으면 그만..
common = 0
while 1 < n2:
if par[n2] in p1:
common = par[n2]
break
else:
n2 = par[n2]
# 서브트리의 개수 구하기
cnt = 0
subtreeCnt(common)
print(f'#{test_case} {common} {cnt}')
SWEA_11315_오목판정
SW Expert Academy
SW 프로그래밍 역량 강화에 도움이 되는 다양한 학습 컨텐츠를 확인하세요!
swexpertacademy.com
문제
N X N 크기의 판이 있다. 판의 각 칸에는 돌이 있거나 없을 수 있다. 돌이 가로, 세로, 대각선 중 하나의 방향으로 다섯 개 이상 연속한 부분이 있는지 없는지 판정하는 프로그램을 작성하라.
입력
첫 번째 줄에 테스트 케이스의 수 T가 주어진다.
각 테스트 케이스의 첫 번째 줄에는 하나의 정수 N(5 ≤ N ≤ 20)이 주어진다.
다음 N개의 줄의 각 줄에는 길이 N인 문자열이 주어진다. 각 문자는 ‘o’또는 ‘.’으로, ‘o’는 돌이 있는 칸을 의미하고, ‘.’는 돌이 없는 칸을 의미한다.
출력
각 테스트 케이스 마다 돌이 다섯 개 이상 연속한 부분이 있으면 “YES”를, 아니면 “NO”를 출력한다.
코드
import sys
sys.stdin = open('11315_input.txt', 'r')
T = int(input())
def omok():
for i in range(N):
for j in range(N):
# 돌을 발견하면
if arr[i][j] == 'o':
for di, dj in d:
ni, nj = i + di, j + dj
cnt = 1
# 주변에 돌을 발견하면 현재 델타 그대로 돌이 나오지 않을 때까지 조회하면서 카운트
while 0 <= ni < N and 0 <= nj < N and arr[ni][nj] == 'o':
ni += di
nj += dj
cnt += 1
# 다섯개 이상 연속한 부분이 있으면 True
if cnt >= 5:
return True
return False
for test_case in range(1, T+1):
N = int(input())
arr = [list(input()) for _ in range(N)]
# 위로 가거나 왼쪽 아래로 내려가는 방향은 필요없어,,왜냐면 위쪽에서 부터 탐색하기 때문
d = [[0, 1], [1, 0], [1, 1], [1, -1]]
if omok():
print(f'#{test_case} YES')
else:
print(f'#{test_case} NO')얼떨결에 pass 한 문제,,,ㅎ 오목 함수 안이 잘 짜여진건지 모를일,,, 조만간 다시 풀어보기,,

교육장 입구에서 찍은 하늘. 교육장으로 오는 길 중에 가장 좋아하는 구간이다.
주변에 높은 건물이 없어서 하늘이 얼마나 높고 넓은지 알 수 있어서 좋아.
답답했던 마음도 괜히 뻥 뚫리는 것 같고?
'Algorithm > SWEA' 카테고리의 다른 글
| SWEA_5188_최소합, SWEA_5189_전자카트 (0) | 2022.09.22 |
|---|---|
| SWEA_4615_재미있는오셀로게임, SWEA_2117_홈방범서비스 (0) | 2022.09.16 |
| SWEA_5117_이진 힙, SWEA_1232_사칙연산 (0) | 2022.09.13 |
| SWEA_5178_노드의합, SWEA_5174_subtree, SWEA_5716_이진탐색 (0) | 2022.09.12 |
| SWEA_12712_파리퇴치3, SWEA_9489_고대유적 (0) | 2022.08.29 |




댓글