SW Expert Academy
SW 프로그래밍 역량 강화에 도움이 되는 다양한 학습 컨텐츠를 확인하세요!
swexpertacademy.com
SWEA_5174_subtree
문제
트리의 일부를 서브 트리라고 한다. 주어진 이진 트리에서 노드 N을 루트로 하는 서브 트리에 속한 노드의 개수를 알아내는 프로그램을 만드시오.

주어지는 트리는 부모와 자식 노드 번호 사이에 특별한 규칙이 없고, 부모가 없는 노드가 전체의 루트 노드가 된다.
이런 경우의 트리는 부모 노드를 인덱스로 다음과 같은 방법으로 나타낼 수 있다. 자식 노드가 0인 경우는 노드가 자식이 없는 경우이다.
입력
첫 줄에 테스트케이스의 수 T가 주어진다. 1<=T<=50
다음 줄부터 테스트 케이스의 별로 첫 줄에 간선의 개수 E와 N이 주어지고, 다음 줄에 E개의 부모 자식 노드 번호 쌍이 주어진다.
노드 번호는 1번부터 E+1번까지 존재한다. 1<=E<=1000, 1<=N<=E+1
코드
# import sys
# sys.stdin = open('5174_input.txt', 'r')
T = int(input())
# 중위순회 함수
def inorder(N):
global cnt
if N == 0:
return
# 노드를 방문하면 cnt++
cnt += 1
# 자식노드도 차례로 방문
inorder(left[N])
inorder(right[N])
for test_case in range(1, T+1):
E, N = map(int, input().split())
inputV = list(map(int, input().split()))
cnt = 0
left = [0] * (E+2)
right = [0] * (E+2)
for i in range(0, len(inputV), 2):
# 왼쪽 자식 노드에 값이 없으면 삽입
if left[inputV[i]] == 0:
left[inputV[i]] = inputV[i + 1]
# 아니면 오른쪽에 삽입
else:
right[inputV[i]] = inputV[i + 1]
inorder(N)
print(f'#{test_case} {cnt}')
SW Expert Academy
SW 프로그래밍 역량 강화에 도움이 되는 다양한 학습 컨텐츠를 확인하세요!
swexpertacademy.com
SWEA_5178_노드의합
문제
완전 이진 트리의 리프 노드에 1000이하의 자연수가 저장되어 있고, 리프 노드를 제외한 노드에는 자식 노드에 저장된 값의 합이 들어있다고 한다.
N개의 노드를 갖는 완전 이진 트리의 노드 번호는 루트가 1번이 되며, 같은 단계에서는 왼쪽에서 오른쪽으로 증가, 단계가 꽉 차면 다음단계의 왼쪽부터 시작된다.
완전 이진 트리의 특성상 1번부터 N번까지 빠지는 노드 번호는 없다.
리프 노드의 번호와 저장된 값이 주어지면 나머지 노드에 자식 노드 값의 합을 저장한 다음, 지정한 노드 번호에 저장된 값을 출력하는 프로그램을 작성 하시오.
입력
첫 줄에 테스트케이스의 수 T가 주어진다. 1<=T<=50
다음 줄부터 테스트 케이스의 별로 노드의 개수 N과 리프 노드의 개수 M, 값을 출력할 노드 번호 L이 주어지고, 다음 줄부터 M개의 줄에 걸쳐 리프 노드 번호와 1000이하의 자연수가 주어진다.
코드
# import sys
# sys.stdin = open('5178_input.txt', 'r')
T = int(input())
for test_case in range(1, T+1):
N, M, L = map(int, input().split())
tree = [0] * (N+1)
for m in range(M):
idx, num = map(int, input().split())
tree[idx] = num
for i in range(N-M, 0, -1):
# 자식노드가 존재할 때만 더해줘
if 2*i <= N:
tree[i] += tree[2*i]
if 2*i + 1 <= N:
tree[i] += tree[2*i + 1]
print(f'#{test_case} {tree[L]}')
SW Expert Academy
SW 프로그래밍 역량 강화에 도움이 되는 다양한 학습 컨텐츠를 확인하세요!
swexpertacademy.com
SWEA_5716_이진탐색
문제
1부터 N까지의 자연수를 이진 탐색 트리에 저장하려고 한다.
이진 탐색 트리는 어떤 경우에도 저장된 값이 왼쪽 서브트리의 루트 <현재 노드 <오른쪽 서브 트리의 루트인 규칙을 만족한다.
추가나 삭제가 없는 경우에는, 완전 이진 트리가 되도록 만들면 효율적인 이진 탐색 트리를 만들수 있다.
다음은 1부터 6까지의 숫자를 완전 이진 트리 형태인 이진 탐색 트리에 저장한 경우이다.

완전 이진 트리의 노드 번호는 루트를 1번으로 하고 아래로 내려가면서 왼쪽에서 오른쪽 순으로 증가한다.
N이 주어졌을 때 완전 이진 트리로 만든 이진 탐색 트리의 루트에 저장된 값과, N/2번 노드(N이 홀수인 경우 소수점 버림)에 저장된 값을 출력하는 프로그램을 만드시오.
입력
첫 줄에 테스트케이스의 수 T가 주어진다. 1<=T<=50
다음 줄부터 테스트 케이스의 별로 N이 주어진다. 1<=N<=1000
해결방법
- 재귀,,,짱 어렵네,,,
직접 그려봤다 ㅎ
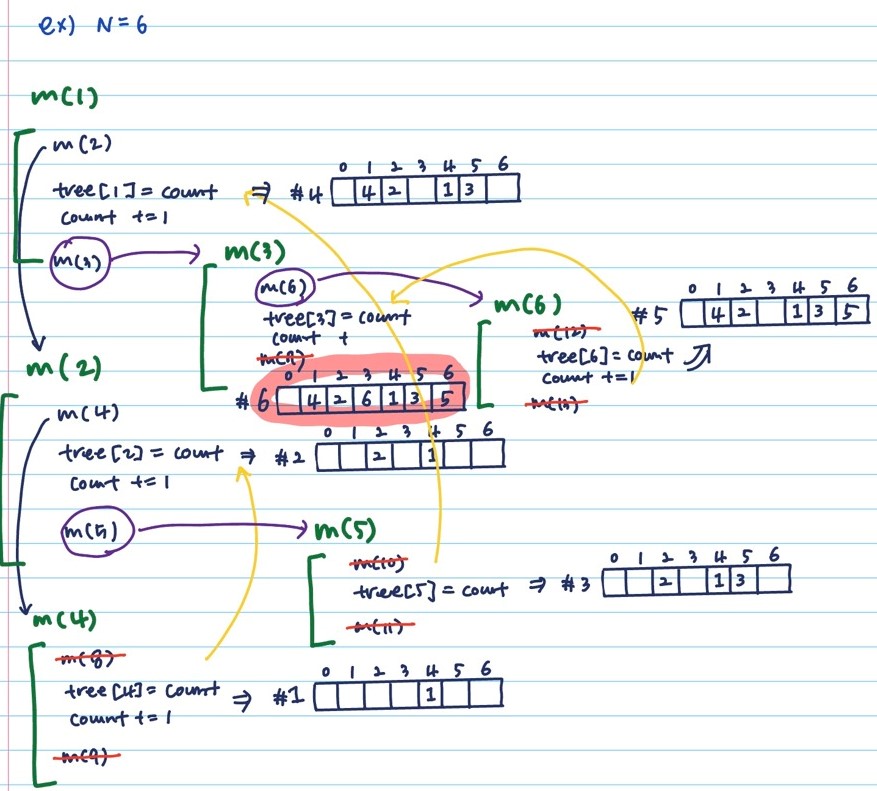
코드
T = int(input())
def inorder(n):
global cnt
if n <= N:
inorder(2*n)
tree[n] = cnt
cnt += 1
inorder(2*n + 1)
for test_case in range(1, T+1):
N = int(input())
tree = [0] * (N+1)
cnt = 1
inorder(1)
print(f'#{test_case} {tree[1]} {tree[N//2]}')

신경쓰고 있는 일이 많은지 편두통이 너무 심한 탓에 식은땀+눈물 흘리면서 예습ㅎ 그래도 하늘사진은 찍어야지.
내일부터 알고리즘 심화 시작!? 진짜진짜 잘해보고 싶어 ㅠ
+ 이제는 컨디션을 잘 조절하는 방법도 고민 해봐야할 것 같다. 오래오래 공부하려면!
'Algorithm > SWEA' 카테고리의 다른 글
| SWEA_4615_재미있는오셀로게임, SWEA_2117_홈방범서비스 (0) | 2022.09.16 |
|---|---|
| SWEA_1248_공통조상, SWEA_11315_오목판정 (0) | 2022.09.15 |
| SWEA_5117_이진 힙, SWEA_1232_사칙연산 (0) | 2022.09.13 |
| SWEA_12712_파리퇴치3, SWEA_9489_고대유적 (0) | 2022.08.29 |
| SWEA_13976_기지국 (0) | 2022.08.28 |




댓글